Content

Events and event spaces

An understanding of sets is crucial for dealing with events and the basic rules of probability: this includes set notation, the subset relationship, and operations on sets such as union and intersection.

The event space \(\mathcal{E}\) is the set of the possible distinct outcomes of the random process. The event space is sometimes called the sample space. When rolling a normal six-sided die and recording the uppermost face, the event space is \(\mathcal{E} = \{1,2,3,4,5,6\}\).

An event is a collection of possible outcomes, and therefore it is a subset of \(\mathcal{E}\). The event \(A\) occurs if the observed outcome is in \(A\), and does not occur if the observed outcome is not in \(A\). It is usual to denote an event by a capital letter, commonly near the start of the alphabet: \(A, B, C, \dots\).

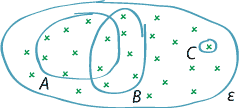
The event space.
Detailed description

Events may be expressed in words, inside quotation marks:

• In the die-rolling example, we can consider the event \(A\) = "a prime number is obtained" = \(\{2,3,5\}\).
• In the example of five people born in 1995, we can consider the event \(B\) = "exactly two of the individuals experience at least one broken leg prior to turning 20".

When expressing an event in words like this, the description must determine a subset of \(\mathcal{E}\). We can regard something as an event only when it is true that, for every possible outcome, we can say definitively whether or not the event has occurred.

An outcome is sometimes called an elementary event.

The following are events in any context:

• The event space \(\mathcal{E}\) is itself an event, because it is a collection of outcomes. We can think of \(\mathcal{E}\) as the event ``quot;the random procedure occurs".
• The empty set \(\varnothing\) is a subset of \(\mathcal{E}\). The event \(\varnothing\) is not very interesting; it contains no outcomes.

The mathematical approach to probability requires that we have to be able to specify the possible outcomes. Outcomes that we may be able to imagine, such as the die coming to rest on a corner (leading to no number being uppermost), are often excluded from consideration altogether. If we do want to consider an outcome as possible, it must be included in the event space.

Recall that the domain of probability statements consists of events. Now that we understand that events are subsets of the event space \(\mathcal{E}\), we see that probability is a set function. It maps subsets of \(\mathcal{E}\) into the interval \([0,1]\).

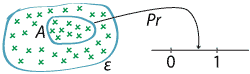
Probability as a set function.
Detailed description

Operations on events and relations between events

Events in random procedures are sets of possible outcomes. We now apply ideas about sets to events; this will help us to think clearly about the events and, subsequently, their probabilities.

For a subset \(A\) of the event space \(\mathcal{E}\), the complementary set is

\[ A' = \{\, x \in \mathcal{E} : x \notin A \,\}. \]

In words, \(A'\) is the set of all elements of the universal set \(\mathcal{E}\) that are not in \(A\).

For the event \(A\), the complementary event is \(A'\). For example:

• In the die-rolling example, if \(A\) = "a prime number is obtained", then \(A' = \{1,4,6\}\).
• In the example of five people born in 1995, if \(B\) = "exactly two of the individuals experience at least one broken leg prior to turning 20", then \(B'\) = "the number of individuals experiencing at least one broken leg prior to turning 20 is 0, 1, 3, 4 or 5".

We are interested in relations between events, and therefore in considering more than one event.

For two events \(A\) and \(B\), the intersection \(A \cap B\) is the event ``quot;\(A\) and \(B\) both occur". In the die-rolling example, if \(A\) = "a prime number is obtained" and \(B\) = "an even number is obtained", then \(A = \{2,3,5\}\) and \(B = \{2,4,6\}\), so \(A \cap B = \{2\}\). As is the case with sets generally, we can consider the intersection of more than two events: the event \(A \cap B \cap C\) is the event ``quot;\(A\) and \(B\) and \(C\) all occur", and so on.

For two events \(A\) and \(B\), the union \(A \cup B\) is the event ``quot;either \(A\) or \(B\) occurs, or both". Equivalently, the union \(A \cup B\) is the event ``quot;at least one of \(A\) and \(B\) occurs". For the die-rolling example again, with \(A = \{2,3,5\}\) and \(B = \{2,4,6\}\), the union is \(A \cup B = \{2,3,4,5,6\}\). We may be interested in the union of more than two events, such as \(A \cup B \cup C\).

We say that an event \(A\) is a subset of an event \(B\), and write \(A \subseteq B\), when all outcomes in \(A\) are also in \(B\). For example, suppose two dice are rolled. If \(A\) = "the sum of the two numbers obtained is 12" and \(B\) = "a six is obtained on the first die", then \(A = \{(6,6)\}\) and \(B = \{(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)\}\), so \(A \subseteq B\).

We say that two events \(A\) and \(B\) are mutually exclusive if their intersection is the empty set, which means they have no outcomes in common. For example, an event \(A\) and its complementary event \(A'\) are mutually exclusive, since \(A'\) consists of all outcomes that are not in \(A\). In the example of five people born in 1995, if we define \(X\) to be the number of individuals experiencing a broken leg prior to turning 20, then the event ``quot;\(X = 1\)" and the event ``quot;\(X = 0\)" are mutually exclusive: they cannot both occur.

Next page - Content - The probability axioms